Chiustin: 4月 2020

2020年4月30日星期四

2020年4月28日星期二

Windows jupyter notebook 發生 InternalError: Blas GEMM launch failed

原因:GPU記憶體不足

解決方式:
from sklearn.preprocessing import RobustScaler
from keras.models import Model, load_model, Sequential
from keras.layers import Input
from keras.layers import LSTM, GRU, Bidirectional, BatchNormalization
from keras.layers import Dense, Dropout
from keras.layers import Concatenate
from keras import regularizers

在import Keras module下方再增加一段程式碼

import tensorflow as tf
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
os.environ["CUDA_DEVICE_ORDER"] = "PCI_BUS_ID"
os.environ["CUDA_VISIBLE_DEVICES"] = '0' # Set to -1 if CPU should be used CPU = -1 , GPU = 0

gpus = tf.config.experimental.list_physical_devices('GPU')
cpus = tf.config.experimental.list_physical_devices('CPU')

if gpus:
    try:
        # Currently, memory growth needs to be the same across GPUs
        for gpu in gpus:
            tf.config.experimental.set_memory_growth(gpu, True)
        logical_gpus = tf.config.experimental.list_logical_devices('GPU')
        print(len(gpus), "Physical GPUs,", len(logical_gpus), "Logical GPUs")
    except RuntimeError as e:
        # Memory growth must be set before GPUs have been initialized
        print(e)
elif cpus:
    try:
        # Currently, memory growth needs to be the same across GPUs
        logical_cpus= tf.config.experimental.list_logical_devices('CPU')
        print(len(cpus), "Physical CPU,", len(logical_cpus), "Logical CPU")
    except RuntimeError as e:
        # Memory growth must be set before GPUs have been initialized
        print(e)

https://github.com/tensorflow/tensorflow/issues/11812

2020年4月27日星期一

Reinforcement-Learning-Algorithms-with-Python github

https://github.com/PacktPublishing/Reinforcement-Learning-Algorithms-with-Python

2020年4月26日星期日

脈衝神經網路(Spiking Neural Networks)

Github
https://blog.csdn.net/xiaoqu001/article/details/78713527

Brian2
https://blog.csdn.net/xiaoqu001/article/details/80422546?utm_source=blogxgwz2

SNN用STDP法的MNIST數據集識別代碼深入閱讀
https://blog.csdn.net/qq_30241709/article/details/79837002

SpikingFlow
https://spikingflow.readthedocs.io/zh_CN/latest/index.html

神經形態計算實現脈衝神經網路

背景

脈衝神經網路(Spiking neural networks, SNNs)是指neuroscientists在研究真正生物的神經網路(例如我們的大腦)時所用的數學模型，由於生物的神經網路實在太複雜了，於是neuroscientists會抽象出許多不同的SNNs模型，來幫助他們了解實際的生物現象。

而對於computer scientists來說，有一群人他們的目標是想要設計出類似大腦神經元的晶片，然後想要能夠比傳統電腦在某些常見的計算問題上，能夠有更快更好的效率。因此他們試圖在SNNs的模型框架之下，設計演算法，想要解決實際的問題。然而在現階段來說，這些都是完全沒有理論支持的。具體來說，沒有理論可以說明為什麼使用SNNs模型可以在這些計算問題上有好的表現，而且即使SNNs在一些模擬中能夠有好的表現，大家也不知道SNNs是怎麼做到的，然後在什麼樣的情況下有可能會表現得很差。

這樣缺乏理論支持的情況，主要是因為SNNs是個看似簡單，但是卻有著非常不連續行為的數學模型。具體來說，讓我們看看一個常見的SNN模型，叫做 integrate-and-fire SNN。在這個模型中，每個神經元(neuron)會有個電位(membrane potential)隨著時間變化。有兩種因子會影響電位的改變，第一種是個固定的外部充電，可以想成是這群神經元以外的東西造成的影響，而為了分析方便，通常我們會先假設這個充電的速率是個穩定不改變的值。第二種影響電位的因子是脈衝(spike)造成的影響。首先在integrate-and-fire SNN中，一個神經元會在他的電位超過閥值的時候，發射一個脈衝(fires a spike)，然後這個脈衝會傳輸到其他的神經元，然後影響它們的電位。這個影響的程度，是根據神經元之間的突觸強度(synapse)來決定的。而在數學模型中，突觸的強度則是簡單的被用一個數字表示。如果現在有n個神經元，那麼最多就會有n^2個突觸(包括神經元自己跟自己的)，而這些數字可以被一個n×n的矩陣記錄起來。

前言

縱觀歷史，創造具有類人腦能力的技術一直都是創新的源泉。從前，科學家們一直以為人腦中的信息是通過不同的通道（通道）和頻率傳遞的，就像無線電一樣。如今，科學家們認為人腦就像一台計算機。通過神經網絡的發展，今天的計算機已在多個認知任務中展現出了非凡的能力，例如，AlphaGo在圍棋戰略遊戲中擊敗了人類運動員。雖然這種表現的確令人印象深刻，但一個關鍵問題仍然存在：這些活動涉及的計算成本有多大？

人腦能夠執行驚人的任務（例如，同時識別多個目標，推理，控制和移動），而能量消耗僅接近2瓦左右。在之下，標準計算機僅識別1000種不同的物體就需要消耗250瓦的能量。儘管人腦尚未被探索窮盡，但從神經科學來看，人腦非凡的能力可歸結於以下三個基本觀察：廣泛的連通性，結構和功能化的組織層次，以及時間依賴（時間依賴）的神經元突觸連接（圖1a）。

神經元（Neurons）是人腦的計算原始元素，它通過離散動作電位（discrete action potentials）或“脈衝”交換和傳遞信息。突觸（synapses）是記憶和學習的基本存儲元素。人腦擁有數十億個神經元網絡，通過數万億個突觸相互連接。基於脈衝的時間處理機制使得稀疏而有效的信息在人腦中傳遞。研究還表明，靈長類動物的視覺系統由分層級的關聯區域組成，這些關聯區域逐漸將視覺對象的映像轉換為一種具有魯棒性的格式，從而促進了感知能力。

目前，最先進的人工智能總體上使用的是這種遭受人腦層次結構和神經突觸框架啟發的神經網絡。實際上，現代深度學習網絡（DLNs）本質上是層級結構的人造物，就像人腦一樣用多個層級去表徵潛在特徵，由來自輸入過程中多個分區的不同潛在特徵的表徵，經過轉換形成的（圖1b）。矽晶體管硬件計算系統是這種神經網絡的硬件基本那些聯想到了人腦的層級結構：各種矽基計算單元以層級方式劃分，以實現高效的數據。交換（圖1c）。

儘管兩者在表面上有相似之處，但人腦的計算原理和矽基計算機之間存在著鮮明的區別。其中包括：（1）計算機中計算（處理單元）和存儲（存儲單元）是分離的，，人類的人腦中計算（神經元）和存儲（突觸）是一體的；（2）串聯於二維連接的計算機硬件，人類腦中的大量存在的三維連通性目前無法在矽基技術上進行模擬；（3）晶體管主要為了建立確定性布爾（數字）電路開關，和人腦基於脈衝的事件驅動型隨機計算不同。雖然如此，在當前的深度學習革命中，矽基計算平台（例如圖像）處理單元（GPU）雲服務器）已成為一個重要的貢獻因素。

但是，通常情況下，在一個由典型的2.1Wh電池供能的嵌入式智能玻璃處理器中（smart-glass processor）上運行深度網絡，就會讓處理器在25分鐘內將電池消耗殆盡。

在人腦的指引下，通過脈衝驅動通信從而實現神經元-突觸計算的硬件系統將可以實現節能型機器智能。神經形態計算始於20世紀80年代晶體管仿照神經元和突觸的功能運行（圖2），之後其迅速演化到包括事件驅動的計算本質（離散的“脈衝”人造物）。最終，在21世紀初期，這種研究努力促進了大規模神經形態芯片的出現。

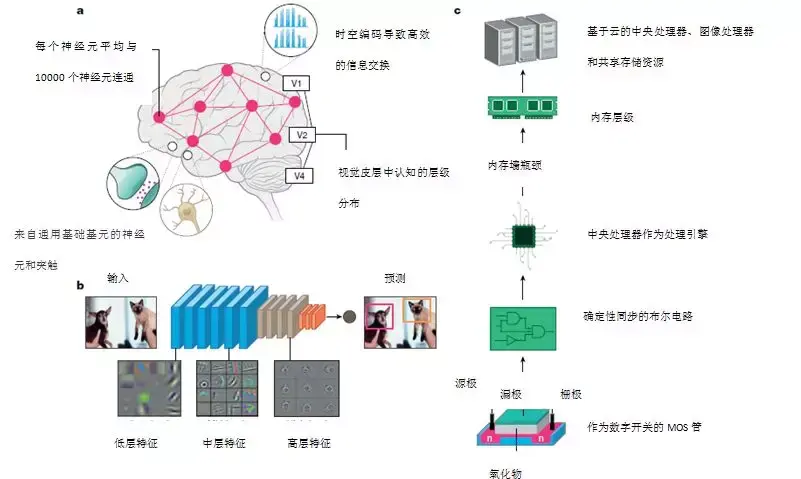
preview

圖1：生物和矽基計算的關鍵屬性構架。a，大腦的組織原理示意圖。神經元和突觸與時間脈衝處理交織在一起的網絡使得不同區域之間的信息能夠快速高效地流動。b，一個深度卷積神經網絡物體執行目標檢測的圖片。這些網絡是多層的，並使用突觸存儲和神經元非線性學習廣泛的數據表示。使用反向傳播訓練後，每層學習的特徵都顯示有趣的模式。第一層學習一般特徵，如邊緣和顏色斑點。轉變我們深入網絡，學習到的功能變得更具體，用對象的部分（如狗的眼睛或鼻子）代表完整的物體（如狗的臉）。這種從一般到特殊的過渡代表了視覺皮層的層次結構。c，最先進的矽計算生態系統。廣義上講，計算層次分為處理單元和內存存儲。處理單元和內存層次結構的物理分離導致“內存牆減小（memory well bottleneck）”。網絡在強大的雲服務器上訓練，儘管會產生巨大的成就，但仍可提供令人驚嘆的精度。

今天，算法設計師們正在積極探索（特別是“學習”）脈衝驅動型計算的優缺點，去推動有可擴展性，高能效的“脈衝神經網絡”（spiking neural networks，SNN）。在這種情況下情況下，我們可以將神經形態計算領域描述為一種協同工作，它在硬件和算法域兩者中權重相同，以實現脈衝型人工智能。我們首先提出了“智能”（算法）方面，包括不同的學習機制（無監督以及基於脈衝的監督，或漸變下降方案），同時突出顯示要利用基於時空事件的表徵。此處討論的重點是視覺相關的應用任務，例如圖像識別和檢測。然後我們將探索“計算”（硬件）方面，包括模擬計算，數字神經運動系統，它們都超越了馮·諾依曼（數字計算系統的最新架構）和芯片技術（代表了基本的場效應晶體管設備，它們是當下計算平台的基礎）。最後，我們將討論算法的硬件協同計前景，說明算法具有用於對抗硬件漏洞的魯棒性，可以實現能耗和精度之間的最佳平衡。

一，算法展望：脈衝神經網絡

脈衝神經網絡

按照，神經元功能，Maass開創性的論文將神經網絡分成三個代際。首先，第一代被稱為McCulloch–Pitt感知機，它執行閾值運算並輸出數字（1、0）。或修正線性單元（ReLU），第二代神經元單元增加了連續非線性，可以實現計算連續的輸出值。第一代和第二代網絡之間的非線性升級在擴展神經網絡向複雜應用和更深度的實現方面起著關鍵作用。當前的DLNs在輸入和輸出之間具有多個隱藏層，都是基於第二代神經元。實際上，由於它們的連續的神經元功能，這些模型可以支持基於梯度下降的反向傳播學習，這也是目前訓練深度神經網絡的標準算法。

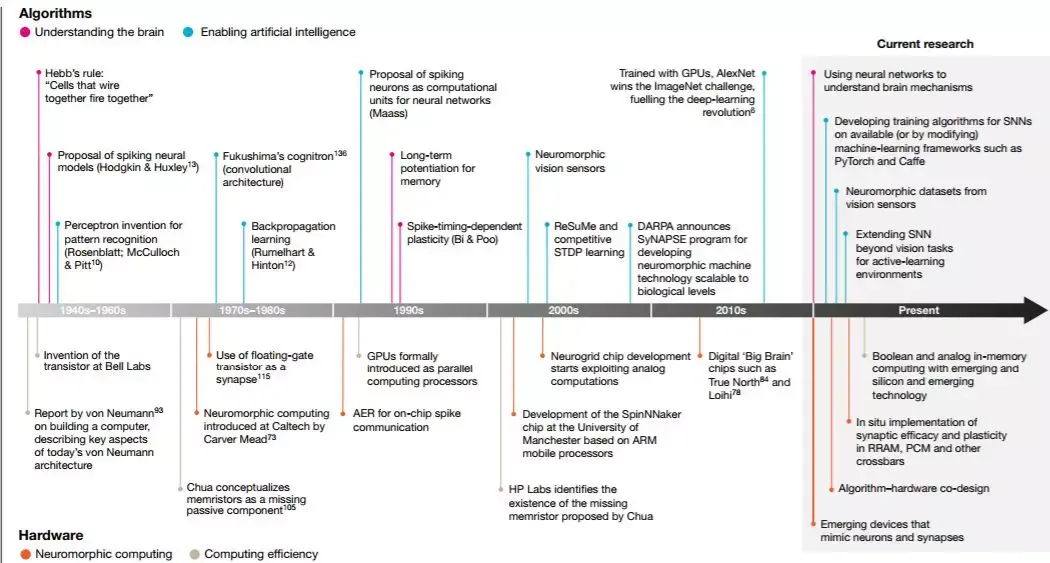
preview

圖2：智能計算的重大發現和進度表（從1940年代到當代）。硬件方面，我們有從兩個角度展示發現：一是對神經形態計算的啟迪，或通過硬件創新實現類人腦的從算法的角度來看，我們已指出這些發現是出於理解人腦的動機，受到神經的影響科學和生物科學的驅動，並同時致力於實現人工智能，它由工程和應用科學所驅動。請注意，這張圖並不是完整或全面的清單。“當前研究”並不一定意味著過去沒有對這些努力進行探索；相反，我們突出了該領域領域和有希望研究的關鍵方面。

第三代神經網絡主要使用“整合放電”（integrate-and-fire）型尖峰神經元，通過脈衝交換信息（圖3）。第二代和第三代神經網絡之間最大的區別在於信息處理性質。第二代神經網絡使用了實值計算（real-value）（例如，信號幅度），而SNN則使用信號的時間（脈衝）處理信息。脈衝本質上是二進制事件，它或者0或者1 。如3a所示，SNNs中的神經元單元僅在接收或發出尖峰信號時才處於活動狀態，因此它是事件驅動型的，因此可以進行節省。如果無事件發生SNNs單元則保持閒置狀態，這與DLNs相反。無論實際值輸入和輸出，DLNs所有單位都處於活動狀態。轉換，SNN中的輸入對應1或0，這也減少了數學上的點積運算ΣiVi×wi（圖3a），突破了求和的計算量。

針對不同的生物保真度水平下產生的脈衝代際，相關的尖峰神經元模型已提出。例如洩漏整合放電型（LIF）（圖3b）和霍奇金-赫克斯利型（Hodgkin–Huxley）。同樣，針對於突觸的可塑性，已有例如赫布型（Hebbian）和非赫布型（non-Hebbian）方案。突觸的可塑性即突觸權重的調節（在SNNs中轉化為學習）取決於突觸前和突觸後尖峰的相對時間（圖3c）。神經形態工程師的一個主要目標是：在利用基於事件（使用基於事件的傳感器）以及數據驅動更新的同時，建立一個具有適當突觸的可塑性的脈衝神經元模型，從而實現高效的識別，推理等智能應用。

今天，我們有相當成熟的神經形態傳感器，來記錄環境實時的動態變化。這些動態感官數據可以與SNNs的時間處理能力相結合，，以實現超低功耗的計算。實際上，與傳統上DLNs使用的幀驅動（frame-driven）的方法比例，SNNs將時間作為附加的輸入尺寸，以稀疏的方式記錄了有價值的信息（圖3），從而實現高效的SNNs框架，並通過計算視覺光流或立體視覺來實現深度感知。結合基於脈衝的學習規則，它可以產生有效的訓練。跟踪和手勢識別的優勢。但是，這些應用程序大多數都使用了DLNs來執行識別。

在這類傳感器中使用SNNs主要改善於缺乏適當的訓練算法，從而可以有效地利用尖峰神經元的時間信息。實際上就精度而言，在大多數學習任務中SNNs的效果仍落後於第二明顯的，尖峰神經元可以實現非連續的信息傳遞，並發出不可微分的離散脈衝（圖3），因此它們不能使用基於梯度下降型的反向傳播技術，而這是傳統神經網絡訓練的基礎。

另外，SNNs仍需要調整為基於脈衝的數據可用性。雖然理想情況下要求SNNs的輸入是帶有時間信息的序列，但是SNNs訓練算法的識別性能是在現有靜態圖像的數據集上進行評估的，例如 CIFAR或ImageNet。然後，此類基於靜態幀的數據將通過適當的編碼技術（例如，編碼編碼或逐步編碼，圖3d）轉換為脈衝序列。雖然編碼技術使我們能夠評估SNN在傳統基準數據集上的性能，但我們要超越靜態圖像分類的任務。結果，我們既沒有良好的基準數據集，也沒有評估SNNs實際性能的指標。收集更多適當的基準數據集的研究，例如動態視覺傳感器數據或駕駛和導航實例，便超越臨界。

（這裡我們指的是作為DLNs的第二代連續神經網絡，以區別於基於脈衝的計算。我們注意到SNN可以在具有捲積層次結構的深度架構上實現，並同時執行尖峰神經元功能。）

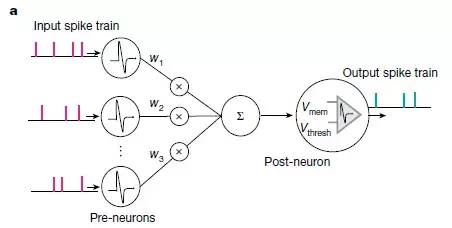
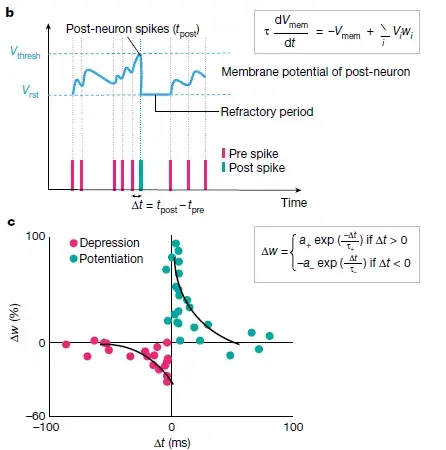
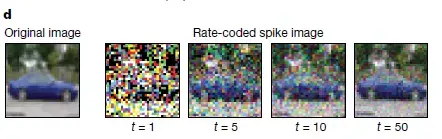
preview

圖3：SNN計算模型。a，上游神經尖峰Vi通過突觸權重wi調節，在給點串聯產生合成電流ΣiVi×wi（相當於點積運算）。產生的合成電流會。由由輸入上游神經元驅動的下游神經元組成的神經網絡。影響下游神經元的膜電位。b，LIF尖峰神經元的動力學顯示。在沒有脈衝的情況下，膜電位Vmem在時間常數τ中集成了脈沖和洩漏。當Vmem超過閾值Vthresh時，下游神經元輸出脈衝。隨之產生不應期(refractory period)，在此期間後神經元的Vmem不再受到影響。c，顯示了基於實驗數據的脈衝時間依賴的可塑性（STDP）公式，其中a +，a-，τ+和τ-是控制權重變化Δw的學習率和時間常數。突觸權重wi根據上游神經元與下游神經元尖峰的時間差（Δt= tpost − tpre）更新。d，使用編碼編碼將輸入圖像（靜態幀數據）轉換為脈沖在各個時間步長上的變換。每個產生一個泊松脈衝序列，其激發速率與預期強度成正比。當幾個時間步求和轉化脈衝映射時（標記為t = 5的脈衝映射是從t = 1到t = 5的映射總和），它們開始輸入。因此，基於脈衝的編碼既保留了輸入圖像的常量，並且在時域中對數據進行了二值化。結果顯示，LIF行為和隨機輸入尖峰的產生使SNN的內部動力學具有隨機性。注意，序列編碼也可以用來生成脈衝數據。

二，在SNNs中學習算法

基於轉換的方法

這種方法的思路是獲得一個SNN，對給定的任務，該SNN將產生與深度神經網絡相同的輸入輸出映射。它的基本原理是，使用權重調整（weight rescaling）和歸一化方法將訓練有素的DLN轉換為SNN，將非線性連續輸出神經元的特徵和尖峰神經元的洩漏時間常數（leak time constants），不應期（refractory period），膜閾值（membrane threshold）等功能相匹配。

實質上，在圖像分類的大型脈衝網絡中（包括ImageNet數據集），這種方法能夠產生了競爭的精確度。在基於轉換的方法中，其優點是無需額外時域中的訓練負擔。 DLN使用了已有的深度學習框架例如Tensorflow對基於幀的數據進行訓練，這些工具提供了訓練中的變換。這種轉換首先需要解析在基於事件的數據（通過對靜態圖像數據集進行速率編碼獲得）上進行訓練的DLN，之後再進行簡單的轉換。

例如，在使用雙曲線正切（tanh）或歸一化指數函數（softmax）後，非線性神經元的輸出值可以得正也可以得負，而脈衝神經元的速率只能是正值。因此，負值總被縮小，導致轉換後的SNNs的精度下降。轉換的另一個問題是在不造成嚴重的性能損失的替代下獲得每一層最佳。的研究提出了確定最佳放電率的實用解決方案，以及在DLNs的訓練過程中約會其他約束（例如噪音或洩漏修正線性單元（leaky ReLUs））以更好地匹配尖脈衝神經元的放電率。今天，轉換的方法可為圖像識別任務提供最先進的精度，並與DLNs的分類性能相當。該的是，從DLNs轉換的SNNs的推理時間變得很長（約幾千個時間步長），導致逐步增加，預期增加。

基於脈衝的方法

在基於脈衝的方法中，SNN使用時間信息進行訓練，因此在整體脈衝動力學中明顯的稀疏性和高效率優勢。研究人員採用了兩種主要方向：無監督學習（沒有標記數據的訓練），以及以及監督學習（有標記數據的訓練）。早期監督學習成果是ReSuMe和tempotron，它們證明了在單層的SNN中，可以使用脈衝時間依賴的可塑性（STDP）的變體去進行分類。從那時起，研究工作一直致力於整合整體脈衝並依次反向傳播的偏差梯度下降法，剎車在多層SNNs中實現監督學習。大多數依賴反向傳播的成果為脈衝神經元功能估計了一個SpikeProp及其相關變體已派生生通過輸出層固定一個目標脈衝序列來實現SNN的反向傳播規則。最近的成果對實值膜電位使用隨機梯度下降法，是為了讓正確輸出神經元隨機激發更的脈衝（而不是具有精確目標的脈衝序列）。這些方法在深度卷積SNNS的小規模圖像識別任務上取得了最新進展，例如美國國家標準與技術研究所（MNIST）手寫數字數據庫的數字分類。

然而，儘管計算效率更高，監督學習在大型任務的精度上卻無法超過採用轉換的方法。而是，受到神經科學和硬件效率為主要目標的啟發，基於STDP學習規則的局部無監督SNN訓練也很有意思。通過局部學習（我們將在後面的硬件討論中看到），有機合成記憶（突觸存儲）和計算（神經元輸出）更緊密地相結合。這種架構更像人 Diehl等人率先證明了完全無監督的SNN學習，其精度可與MNIST數據庫深度學習相區分美（圖4b）。

但是，將局部學習方法擴展到多層複雜任務是一個挑戰。以及網絡的深度，神經元的放電率會降低，我們稱為“消失的前向脈衝傳播”。為了避免這種情況，多數工作用逐層的方式訓練多層SNN（包括卷積SNNs）在局部的脈衝學習模式，然後進行雙向學習反向傳播學習，以去進行分類。但在分類精度方面仍落後於轉換的方法。以及，最近的成果顯示了概念驗證，即通過深度SNNs中反饋連接錯誤信號的隨機投影確實改善了學習。這種基於反饋的學習方法需要進一步研究，以評估其在大規模任務上的效果。

對二元製學習的啟示

我們可以通過僅用二進制（1/0）位值，而不是需要額外的內存的16位或32位浮點值來獲得超低開銷和高效的計算。實際上在算法層級，目前正在研究以概率方式學習（關於神經元何時隨機突跳，權重的轉換精度何時變低）獲得參數對準的網絡和計算操作。二元和三元的DLNs也被提出，其神經元輸出和權重只取低精度值-1、0和+1，而且在大規模分類任務中表現良好。基於二進制脈衝處理模式，SNN已具有計算優勢。轉化，LIF神經元的神經元動力學中的隨機性可以顧及外部噪聲（例如，有噪聲的輸入或有噪聲權重的硬件參數），來提高網絡的魯棒性。那麼，我們是否可以使用結合此SNN時間處理架構使用適當的學習方法，從而將權重訓練壓縮為二進制，使精度損失最小，還有待研究。

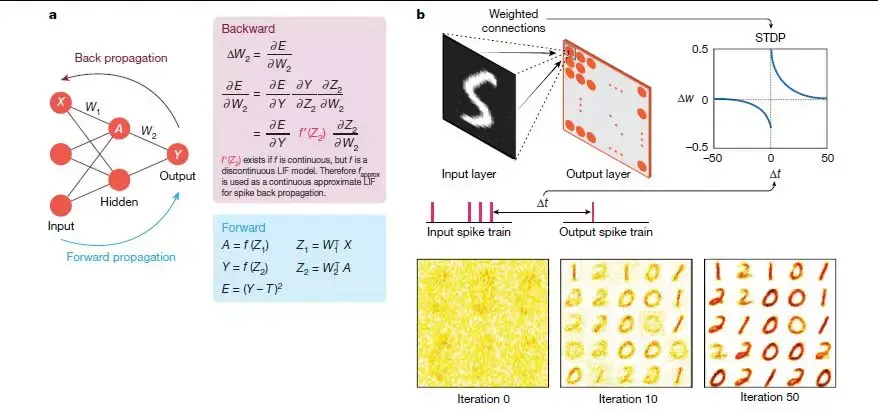
preview

圖4：尖峰網絡中的各個層次和局部學習原理。a，在已知目標標籤指導下進行分類學習，T進行分類任務。給定一個前饋網絡，網絡通過隱藏層單位A向前傳播輸入值X，並輸出神經元激活值Y。結合非線性變換ƒ（Z1），使用輸入的加權求和可以計算隱藏層的A，用矩陣符號表示為Z1 = W1 TX。以類似的方式進行計算。然後，用誤差相對於權重（W1，W2）的導數E求出隨後的權重更新。前向和反向傳播的依次導致學習。誤差求導需要ƒ'，這要求ƒ'是連續的。因此， b，局部STDP數字分類無監督學習。給定一個兩層拓撲結構，輸入層與輸出層的所有神經元完全連接，通過STDP學習突觸連接。根據輸入層和輸出層神經元的尖峰時間差異進行權重調整。輸入神經元在輸出之前（或然後在多個時間步長上進行訓練，權重在初始化時隨機賦值，通過訓練學習對一類輸入所示的樣式進行通用表示的編碼（在這種情況下為“ 0”，“ 1”和“ 2”）。這裡，為了進行識別，目標標籤是不需要的。

三，其他有待研究的方向

超越視覺任務

SNN也可以處理序列數據，但是並沒有研究論證SNN在處理NLP的能力，那麼，我們已經確定了大多數分類任務處理的方法，那麼如何處理在靜態圖像上識別和推理之外的任務呢？。使用SNN做因果預測的能力又如何呢？？深度學習指向在強化學習領域做出改善的研究[62,63]，不過使用SNN進行強化學習研究的卻很少。在SNN這一領域-特別是在訓練學習算法中——SNN所面臨的最大挑戰就是否能表現出和深度學習相當的性能。雖然深度學習已經設下了很高的競爭門生物學，但是我們相信SNN會在機器人，自主控制等領域表現的更好。

終身學習和小樣本學習

深度，學習模型在長期學習時會出現災難性遺忘現象。尺寸，學習過任務A的神經網絡在學習任務B時，它會忘記學過的任務A，只記得B。如何在動態的環境中像人這固然是深度學習研究的一個新的方向，但我們應該探究給SNN增加額外的時間維度是否實現持續性學習型任務。另一個類似的任務就是，利用少量數據進行學習，這也是SNN能超過深度學習的領域。SNN中的無監督學習可以與提供少量數據的監督學習相結合，只使用一小部分標記的訓練數據得到高效的訓練結果[46,50,65]。

與神經科學建立聯繫

我們可以和神經科學的研究成果相結合，把這些抽象的結果應用到學習規則中，從而提高學習效率。例如，Masquelier等人[65]利用STDP和時間編碼模擬視覺神經皮層，他們發現不同的研究者把樹突學習[66]和結構可塑性[67]結合起來，把樹突的連接數做為一個超-[神經元能學習到不同的特徵，這一點點卷積層學到不同的特徵。參數，逐步為學習提供更多的可能。SNN領域的補充互補研究是LSM（liquid state machines）[68]。LSM利用的是法定培訓，隨機鏈接的遞歸歸網絡框架，該網絡對序列識別任務表現卓著[69–71]。但是在復雜的大規模任務上的表現能力仍然有待提高。

四，硬件展望

從前文對信息處理能力和脈衝通信的描述中，我們容易假設設置一個類似的能力的硬件系統。這套系統能夠成為SNN的重疊計算框架。在生物大腦中無處不在的神經元和突觸的啟發，設計出緊密結合在一起的計算和記憶結構；以及實現更複雜的功能-例如，使用最少的電路元件來模擬神經元與突觸動力學。

神經形態計算的出現

在20世紀80年代，晶體管發明了40年後，在生物神經系統領域，Carver Mead預測了“更智能”，“更高效”的矽基計算機結構[72,73]。他也表示過自己最初試圖建立神經系統的嘗試是“簡單而愚蠢的” [74]。但是他的工作代表了計算硬件領域的一種新的範式。Mead並非在意AND，OR等布爾運算[74]。相反他利用金屬氧化物矽（MOS）晶體管在亞閾值區的電氣物理特性（電壓-電流指數相關）來模擬指數神經元的動力學特徵[72]。這樣的設備-傳遞協同設計是神經形態計算中最有趣的領域之一。

並行GPU的出現

和CPU這種由一個或多個處理複雜任務的芯片組成的計算核心不同，GPU [75]是由多個可以進行並行計算的簡單計算核心組成。因此能完成高並發，高吞吐的任務。在傳統意義上GPU是加速圖形應用程序的硬件加速器，但是現在有很多的非圖形應用都受益於GPU的特性。深度學習就是一個顯著的例子[6]，其實GPU只是深度神經網絡的首選平台，也是SNN訓練的平台[76,77]。雖然GPU在高擴展性上發揮優勢，但無法很好的進行進行基於事件驅動的脈衝計算。因此，事件驅動的“超級大腦”神經芯片就可以提供高效的解決方案[78,79]。

“超級大腦”芯片

“超級大腦”芯片[80]的特點是整合了百萬計的神經元和突觸，神經元和突觸提供了脈衝計算的能力[78,81–86]。Neurogrid [82]和TrueNorth [84]分別是基於混合信號模擬電路和數字電路的兩個模型芯片。Neurogrid使用數字電路，因為模擬電路容易累積錯誤，並且芯片製造過程中的錯誤影響也無法克服。設計神經網絡預測幫助科學家模擬大腦活動，通過複雜的神經元運作機制-類似離子通道的開啟和關閉，以及突觸特有的生物行為[82,87]。TrueNorth作為一種神經芯片，目的是用於重要的商業任務，例如使用SNN分類識別任務；而且TrueNorth是基於簡化的神經科突觸原型來設計的。

以TrueNorth為例，主要特性如下[78,88]：

異步地址事件表示（異步地址事件表示）：首先，異步地址事件表示相應的傳統的芯片設計，在傳統的芯片設計中，所有的計算都按照時序時鐘進行，但是因為SNN是稀疏的，僅當脈衝產生時才要進行計算，所以異步事件驅動的計算模式更加適合進行脈衝計算[89,90]。

芯片網絡：芯片網絡（networks-on-chip，NOC）可以用作脈衝通信，NOC就是芯片上的路由器網絡，通過時分複用技術用總線收發數據包。大規模芯片必須使用NOC，是因為在矽片加工的過程中，連接主要是二維的，在第三個維度靈活程度有限。也要注意到，儘管使用了NOC但芯片的聯通程度，仍然不能和大腦中的三維連通性分數。包括TrueNorth內置的大規模數字神經芯片，某些Loihi [78]，已經展示除了SNN技術以外的應用效果。由於我們能更接近生物仿真技術。不過，有限的連通性，NOC總線的限制，和全數字方法仍然需要進一步的研究。

超越馮·諾依曼式計算

晶體管尺寸規模的持續行距縮小的現像被稱為摩爾定律[91]，摩爾定律推動了CPU和GPU以及“超級大腦”芯片的不斷發展。不過近幾年，採用矽基晶體管接近物理極限，這一發展速度指標[92]。為了適應現代人類對計算能力的不斷提升，研究者們設計出了一種雙管齊下的方法，導致“超馮·諾依曼”，“超矽”計算模型成為了可能，馮·諾依曼模型的一大特徵就是，存儲單元和運算單元的分離[93]。通過系統總線傳輸數據。因此，數據在高速的運算單元和低速的存儲單元之間的交替傳輸就成為了預期的“存儲牆瓶頸”（memory wall bottleneck）。這一時期限制了計算的吞吐和效率[94]。

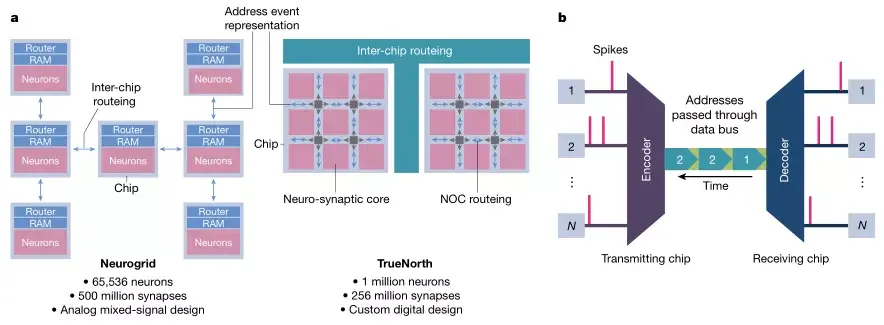
preview

圖5：一些有預期的“超級大腦”芯片和AER方法

A，Neurogrid具有65,000個神經元和5億個突觸，而TrueNorth則具有100萬神經元和2.56億個突觸。Neurogrid和TrueNorth分別使用樹和網格路由拓撲兩種結構。Neurogrid使用模擬混合信號通常來說，像TrueNorth這樣的數字神經形態系統將神經元的膜電位表示為n位二進制格式。通過適當增加或減少n位字來實現神經元動力學，採用LIF行為。根據之下，模擬系統將膜電位表示為存儲在電容中的寄生。通過電流從電容進出，模擬所需的神經元動力學。儘管存在電路差異，但一般來說，模擬系統和數字系統驅動程序是實現低功耗大規模集成系統的關鍵。

B，基本的AER通信系統。每當發射端送出一個事件（一個脈衝），相應的地址就通過數據總線發送到接收端。接收端解碼輸入地址，並重新構造脈衝的序列。因此，每個脈衝由其位置（地址）顯式編碼，並在其地址發送到數據總線時隱式編碼。

改進這一措施影響的方法就是使用“近內存（near-memory）”，“內存中”計算[95,96]。近內存計算是通過在內存單元附近嵌入一個專門的處理器，實現內存的實際上，各種“超級大腦芯片”的分佈式計算體系結構所具有的緊密放置的神經元和突觸分佈就是近內存計算的表現。相比較而言，內存中計算則是把部分計算操作嵌入到內存內部或外部電路中。

初步性技術

初始性技術（ non-volatile technology）[97–103]通常被用於與生物突觸相比較。實際上，它們展示了生物突觸的兩個特徵：突觸效能（突觸功效）和突觸可塑性（ synaptic plasticity）。突觸可塑性指的是根據特定的學習規則調整突觸權重的能力。突觸效能指的是根據輸入脈衝產生輸出的現象。以最簡單的形式來說，意思是說，從上游神經元得到的信號，相乘再求和後再作用於下游神經元的輸入。後文的圖片就說明了，如何使用新興的非易失性憶阻技術（ non-volatile memristive technology）實現突觸效率和突觸可塑性[103,104]。而且，還可以通過時間驅動NOC的方式了連接開關，從而構建密集大規模的神經處理器，以實現內存中計算。

一些已經發表過的基於憶阻技術的研究[105,106]，可變可變電阻式內存（RRAM）[107]，相變內存（PCM）[108]，和自旋傳遞磁盤磁性隨機讀寫器（STT-MRAM）[109]，已經在原位點積和基於STDP規則的突觸學習中進行了探索。RRAM（氧化物基和導電橋基[107]）是電場驅動器件，有助於絲極的形成來RMS容易出現因設備，因週期的變化[110,111]，這是這一技術的主要障礙。PCMS包括夾在兩個電極之間的硫系材料，可以在非晶態（高電阻）和晶態（低電阻）之間的轉換。PCM設備有類似的編程電壓和RRAM的寫入速度，不過這種器件也會受到高寫入電流和串聯電阻漂移的影響[108]。自旋電子器件是由兩塊墊片偏置的電磁組成，依據兩層的磁化方向是平行還是反平行，能呈現兩種電磁狀態。與RRAM和PCM比例，自旋裝置顯示出幾乎無限的加速度。，逐步的寫入能量和異步，在自旋器件中，兩個極端電阻態（ON / OFF）的比率要比在PCM和RRAM中小幅度。

另一類包含可調電阻性電阻的插入性器件是浮柵晶體管（floating-gate transistor）。此類設備有作為突觸觸發器的潛力[112–114]。實際上浮柵晶體管是第因為，他們與MOS製造工藝的相容，比其他新型器件的生產技術更加成熟，然而，與其他替代性技術劃分，浮柵晶體管的主要缺點是耐用性低和編程電壓高。

雖然原位計算（situ computing）和突觸學習為規模超越馮·諾依曼分佈式計算提供了誘人的前景，但有很多挑戰仍然有待克服，因設備，因週期和進展相關引起的變化，計算的近似性質容易出現錯誤，從而減低整體的計算效率，最終影響精確度。轉換，交叉開關操作的魯棒性受到電流潛入通路，線電阻，驅動電路的源電阻和感測電阻的存在的影響[117,118]。選擇器（晶體管或雙端非線性裝置）的非理想性，對模擬-數字轉換設備的要求和有限的比特精度要求，也增加了使用非傳統突觸裝置設計可靠計算的總體複雜性。總體而言，插入初始性設備通常會消耗大量的資源。而且，此類設備的固有隨機性會導致不可靠的寫操作，又需要代價高昂的檢驗方案[119]。

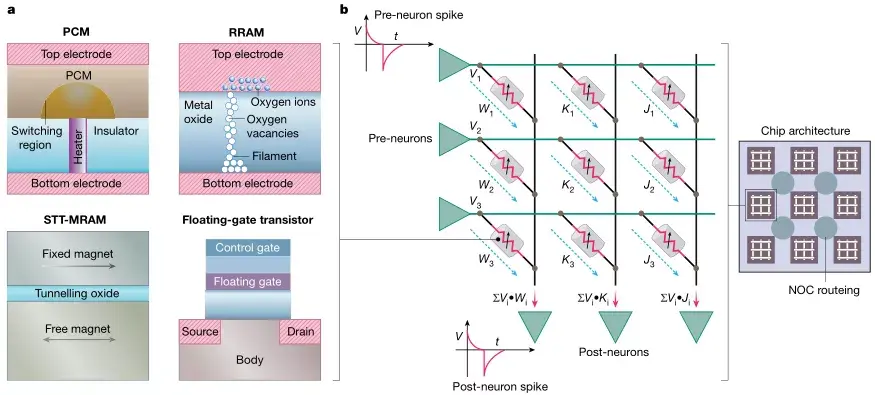
preview

圖6：使用複位性存儲設備作為突觸存儲器件。A，各種複位性技術的原理圖：PCM，RRAM，STT-MRAM和浮柵晶體管。這種替代性設備已經被利用突觸存儲和原位神經突觸計算，以及通用非神經形態變量內部加速器。B，用憶阻技術實現突觸效能和突觸可塑性。圖展示了以交叉方式連接的憶阻器陣列。根據歐姆定律，水平線（綠色）上的輸入脈衝產生與憶阻元件電導成比例的電流。又因為基爾霍夫電流定律，與通過多個峰前神經元的電流垂直線（黑色）相加。此操作表示出了突觸效率的內存中點積運算。通常，只要神經元前和後尖峰分別在水平線和垂直線上（如在STDP），突觸可塑性就可以通過適當地施加電壓脈衝來原位實現。組成憶阻器的電阻值是根據相應的水平和垂直線上產生的電壓差編程的。根據特定的器件技術，再選擇要編程電壓脈衝的形狀和定時。請注意，浮柵晶體管是三端子器件，因此需要額外的水平線和（或）垂直線來實現交叉開關功能。該圖還顯示了以平鋪方式連接NOC的憶阻陣列，可以實現高碳化的原位計算

矽（內存中）計算

除了上述性技術之外，各種使用標準矽存儲器（包括靜態和動態隨機存取存儲器）進行內存計算的預測均值在研究中。這些工作主要集中在把布爾向量計算嵌套內存中[120–122]。常量，混合信號模擬內存計算操作和二進製卷積操作最近被證明是可行的[123,124]。事實上，目前幾乎所有主要的內存技術都在探索各種形式的內存計算，包括靜態內存[125]和動態內存[126]，RRAM [127]，PCM [128]和STT-MRAM [129]。這些這些工作大部分集中在常見的計算應用上，如加密和深度神經網絡，但他們也可以輕鬆的一直到SNN上來。

五，算法-硬件協同設計

混合信號模擬計算

模擬計算容易受到過程引起的變化和噪聲的影響，以及由於模擬和數字轉換設備的複雜性和精度要求，在面積和方面方面受到了很大的限制。將芯片學習與緊密結合的模擬計算框架在過去的[130,131]以及近期的可行生物算法的研究[54]中，已經研究了以芯片上（on-chip）和設備上（on-device）學習解決方案為重點的局部學習。本質上，無論是局部學習這種形式還是樹突襲這種範式，我們都認為，更好的容錯局部學習算法-即使是要學習額外的參數-將是推動模擬神經形態計算的關鍵所在。以及，芯片上學習的適應能力可在不降低目標精度的替代下，開發尺寸的近似模數轉換器。

憶阻點積

作為模擬計算的一個實例，憶阻點積（Memristive dot products）是實現原位神經形態計算的一種有前景的方法。不幸的是，表示點積的憶阻陣列中產生的電流既有空間依賴性又有數據誤差，這導致交叉開關電路分析成為一個非常複雜的問題。研究交叉開關電路非理想狀態的影響[117,132,133]，探索消除點積不准確影響的訓練方法的研究並不多[118,134 ]。而且，這些工作大部分集中在深度神經網絡而不是SNN中。然而，我們可以合理地假設，在這些工作中開發出的基本器件和對電路的見解也能用於SNN的實現。的工作需要精緻的設備-通道模擬運行，必須與訓練算法緊密替換，以減少精度損失。我們認為，基於最新設備的交叉開關佈局的理論模型，以及為點積誤差建立理論邊界的努力，都這將使算法設計者無需耗時，設計異步設備-通路-法模擬，就能探索新的訓練算法，同時也能解決硬件不一致的問題。

随机性

隨機SNN引起了人們極大的興趣，這是因為新興的設備本身俱有隨機性[135,136]。隨機二進制SNN的實現結果，大多數都集中在MNIST數字識別之類的小規模任務上[56]。認為，即使在二元條件下，STDP學習中的時間維度權重更新提供了額外的額外，是的整體朝著真確的方向前進（總體精度）。這種二元局部學習方案與基於梯度下降的擴展學習規則相結合，在利用了硬件隨機性的同時，為高能效神經系統提供了有利的機會。

混合設計方法

我們認為，基於混合方法的硬件解決方案-即在單一平台上結合各種技術的優勢-是另一個需要深入研究的重要領域。這種方法可以在最近的文獻中找到[137]，某種，把低精度憶阻器與高精度數字處理器結合使用。這種混合方法有很多可能的變體，包括顯著驅動的計算數據分離，混合精度計算[137]，將常規矽存儲器重新配置為需內存近似加速器[125]，局部同步和異步設計[138]，局部模擬和串行數字系統；其中新興技術和傳統技術可以同時使用，以提高精確度和效率。混合脈衝學習的方法結合使用，例如局部無監督學習，然後是一系列有監督反向傳播算法[53]。我們認為，這種局部-相互學習方案可以利用降低硬件複雜性，同時，替代的減少對終端應用程序的性能影響。

六，總結

如今，“智能化”已經成為了我們周圍所有學科的主題。在這方面，此處所說的神經形態計算作為一種高效方式，通過硬件（計算）和算法（智能）的協同演進的方式來實現機器智能。

我們首先討論了脈衝神經範式的算法含義，這種範式使用事件驅動計算，而不是傳統深度學習範式中的數值計算。描述了實現標準分類任務的學習規則（例如基於脈衝的梯度下降，無監督STDP和從深度學習到脈沖模型的轉換方法）的優點和局限性。

未來的算法研究應該利用基於脈衝信號的信息處理的稀疏和時間動態特性；以及可以產生實時識別的互補神經形態學數據集；硬件開發應該側重於事件驅動的計算，內存和計算單元的協調，以及模擬神經突觸的動態特徵。特別引人關注的是新興的初始化性技術，隨後技術支持了原位混合信號的模擬計算。我們也討論了包含算法-硬件協同設計的跨層優化的前景。例如，利用算法適應性（局部學習）和硬件可行性（實現隨機脈衝）。

最後，我們認為，基於傳統和新興設備內置的基於脈衝的節能智能係統與當前無處不在的人工智能對比，兩者的前景其實是相吻合的。現在是我們該交換理念的時候了，通過設備，通路，架構和算法等多學科的努力，通力合作打造一台真正節能且智能的機器。

參考
https://www.nature.com/articles/s41586-019-1677-2
file:///C:/Users/PPCC/Downloads/acsami.5b08541.pdf
file:///C:/Users/PPCC/Downloads/acsnano.6b07894.pdf
https://pubs.acs.org/doi/full/10.1021/acsnano.8b03831#
https://zhuanlan.zhihu.com/p/94556277

Announcing PyCaret 1.0.0-An open source low-code machine learning library in Python

https://towardsdatascience.com/announcing-pycaret-an-open-source-low-code-machine-learning-library-in-python-4a1f1aad8d46

2020年4月24日星期五

A detailed explanation on Ordinary least square regression

https://www.dataspoof.info/post/a-detailed-explanation-on-ordinary-least-square-regression?fbclid=IwAR1YWod6w0SmBvZctXIrD7d1Ai-4RsDu5-lfoyNwC9BOfog0KHkUw9VCw9w

Nature biotechnology 全新降維視覺化方法 PHATE

美國耶魯大學發表新的降維視覺化方法 PHATE，以資料點間的幾何距離來突顯 local 與 global 非線性結構。隨著許多不同類型的高維度生物資料產生，如何能保留生物資料中重要且感興趣的結構並視覺化顯得相當重要。目前常見的降維方法如 PCA 與 t-SNE，但其對 noise 相當敏感，而生物醫學資料存在許多雜訊導致可能無法識別精細的局部結構，再者非線性方法(如 t-SNE)通常會擾亂資料的全域結構。
作者將 PHATE 與其他降維工具 (PCA、Diffusion maps、t-SNE、lsomap、Force-directed layout、UMAP、Monocle2) 以 5 份 scRNA 資料集分析比較，結果顯示 PHATE 能有效解決細胞異質性及保留資料的特性，包括連續性過程、分枝(branch)和聚類分析，其中許多分支與作者驗證的細胞類型或 cluster 一致 (亦存在於 Force-directed & t-SNE)，但在 Force-directed layout 往往會產生帶有較少分支的視覺化效果，此外，t-SNE 傾向於將軌跡打碎成 clusters，以至於無法真實呈現資料中的 natural clusters。
PHATE 可適用於各種生物資料型態，包含基因體表型分析、質譜資料、單細胞分析、Hi-C 與微生物體資料等，作者希望透過 PHATE 提供新的大規模高維度資料視覺化工具，徹底改變生物醫學數據的探索方式。

https://www.nature.com/articles/s41587-019-0336-3?fbclid=IwAR3pUGj04BKwhmYh-_NOW1XTxPOcrmu-LjIbEVf6aA1JRtR4--axUUZb0r0