化學信息學的第一步是將分子結構轉變為可以由計算機處理的東西。目前,尚不存在能夠捕獲化合物具有的所有信息的已知表達方法,因此有必要根據後續分析的興趣來決定應保留化合物的哪些信息以及應丟棄哪些信息。您需要對其進行轉換。
這次我們要處理的
“庫侖矩陣”也是表達分子的方式之一。特別
基於的信息,實現了分子的平移和旋轉操作的不變轉換。
在發表QM7數據集的論文中報告了庫侖矩陣。 QM7的原始論文為以下論文。
“Fast and Accurate Modeling of Molecular Atomization Energies with Machine Learning”, Phys. Rev. Lett. 2012, 108, 058301.
目錄
1. 什麼是庫侖矩陣
2. 使用RDKit計算庫侖矩陣
3. 庫侖矩陣計算的實現
4. 使用庫侖矩陣判斷分子相似性
4.1 分子間距離的實現
4.2 用庫侖矩陣可視化QM7數據集中的化學空間
5. 隨機庫侖矩陣
6. 結論
什麼是庫侖矩陣
在文章“化學空間項目和GDB數據庫”中引入的GB13數據庫包含使用PBE0優化的結構和能量,PBE0是具有7個或更少重原子的分子的雜合功能。是QM7數據集。
發表QM7的論文的作者估計能量被用作輸入,因為“從Schrodinger方程獲得分子能量所需的信息是分子中所有原子的類型和坐標”。我認為有可能建立一個機器學習模型來
基於外部坐標軸的分子的XYZ坐標是用於繪製分子的便捷表達方法,但是對於機器學習模型而言,它們不是優選的表達。這是因為即使同一分子平行旋轉或移動,分子的能量也不會改變,但是這些操作會改變分子的三維坐標。
庫侖矩陣是用於分子平移和旋轉的不變表達方法,
用表示。認為對角元素編碼“原子能”,非對角元素編碼“庫侖斥力”。
注意,根據庫侖矩陣的上述定義,可以通過更改分子中原子的順序來獲得不同的矩陣。
使用RDKit計算庫侖矩陣 (AllChem.CalcCoulombMatrix(mol))
自2020.03更新以來,在RDKit中添加了一種計算庫侖矩陣的方法。通過傳遞RDKit的MOL對象,可以獲得庫倫矩陣作為rdkit.rdBase._vectd對象的元組。在下面的代碼中,計算是在乙醇上執行的,並轉換為numpy數組。
from rdkit import rdBase, Chem
from rdkit.Chem import AllChem
import numpy as np
print('rdkit version: ', rdBase.rdkitVersion)
ethanol = Chem.AddHs(Chem.MolFromSmiles('CCO'))
AllChem.EmbedMolecule(ethanol, AllChem.ETKDG())
np.array(AllChem.CalcCoulombMat(ethanol))
|
array([[36.8581052 , 23.63625731, 20.55037573, 5.37460683, 5.49640183,
5.35417845, 2.73481097, 2.73767777, 2.61195049],
[23.63625731, 36.8581052 , 34.08028911, 2.83778898, 2.7347546 ,
2.83728316, 5.42533149, 5.43607405, 3.0029401 ],
[20.55037573, 34.08028911, 73.51669472, 3.3655073 , 2.42272356,
3.04345175, 3.96763228, 3.95109687, 8.08026531],
[ 5.37460683, 2.83778898, 3.3655073 , 0.5 , 0.5449894 ,
0.55454634, 0.32904401, 0.38921411, 0.46477107],
[ 5.49640183, 2.7347546 , 2.42272356, 0.5449894 , 0.5 ,
0.54292632, 0.36982712, 0.39829825, 0.29588076],
[ 5.35417845, 2.83728316, 3.04345175, 0.55454634, 0.54292632,
0.5 , 0.42263221, 0.32630447, 0.4395109 ],
[ 2.73481097, 5.42533149, 3.96763228, 0.32904401, 0.36982712,
0.42263221, 0.5 , 0.5410353 , 0.39203258],
[ 2.73767777, 5.43607405, 3.95109687, 0.38921411, 0.39829825,
0.32630447, 0.5410353 , 0.5 , 0.35615831],
[ 2.61195049, 3.0029401 , 8.08026531, 0.46477107, 0.29588076,
0.4395109 , 0.39203258, 0.35615831, 0.5 ]])
庫侖矩陣計算實現
RDKit中也實現了庫侖矩陣計算,但是為了更好的理解,我們將在此處實現它。
在下面的代碼中
- get_dist:用於查找RDKit構象對像中指定原子之間的距離的函數
- gen_coulomb_matrix:接收RDKit MOL對象並返回庫侖矩陣作為numpy數組的函數
被實施。通過使用庫侖矩陣的對稱性,減少了後者函數的複雜性。
def get_dist(conf, atomid1, atomid2):
position1 = np.array(conf.GetAtomPosition(atomid1))
position2 = np.array(conf.GetAtomPosition(atomid2))
distance = np.sqrt(np.sum((position1 - position2) ** 2))
return distance
def gen_coulomb_matrix(mol):
conformer = mol.GetConformer(-1)
n_atoms = mol.GetNumAtoms()
arr = np.zeros((n_atoms, n_atoms))
for i in range(n_atoms):
for j in range(n_atoms):
zi = mol.GetAtomWithIdx(i).GetAtomicNum()
zj = mol.GetAtomWithIdx(j).GetAtomicNum()
if i == j:
arr[i,j] = 0.5 * zi ** 2.4
elif i > j:
distance = get_dist(conformer, i, j)
arr[i,j] = zi * zj / distance
arr[j,i] = arr[i,j]
else:
continue
return arr
gen_coulomb_matrix(ethanol)
|
您將獲得與以前相同的矩陣。
使用庫侖矩陣判斷分子相似性
在“使用RDKit使用指紋確定分子相似性”一文中,我們解釋了Tanimoto Coefficient之類的方法,該方法通過使用指紋對分子進行向量化來量化分子之間的相似性和距離。
那麼,如何表達庫侖矩陣表達的分子之間的相似性呢?
該論文的作者定義了一個向量ε,它是按降序排列的庫侖矩陣的特徵值,
並定義了化合物之間的距離。 此時,當比較具有不同原子數的分子時,請用零填充ε以使大小均勻。
通過這樣表達複合空間,
- 每個分子都可以獨特表達
- 對稱原子的貢獻相等(因為它們按降序排列)
- 原子序不變
獲得特徵。
分子間距離的實現 (numpy.linalg.eigvals(ndarray))
現在,讓我們根據以上定義找到距庫侖矩陣的距離。 線性代數關係的運算在numpy.linalg中實現。
在下面的代碼中
get_eigenvalues_from_matrix:生成庫侖矩陣特徵值的向量
get_distance_mols_with_coulomb_matrix:基於庫侖矩陣計算兩個RDKit MOL對象之間的距離
該功能已定義。 在那種情況下,前者通過給出向量長度來執行以零填充的操作。
使用本文最後定義的函數,讓我們找到“乙醇和吡咯”與“吡咯和噻吩”之間的距離。
def get_eigenvalues_from_matrix(mat, dim):
eigenvalues = np.sort(np.linalg.eigvals(mat))[::-1]
if dim > len(mat):
expanded_vec = np.zeros(dim)
expanded_vec[:len(mat)] = eigenvalues
else:
expanded_vec = eigenvalues
return expanded_vec
def get_distance_mols_with_coulomb_matrix(mol1, mol2):
max_n_atoms = max(mol1.GetNumAtoms(), mol2.GetNumAtoms())
mat1 = gen_coulomb_matrix(mol1)
mat2 = gen_coulomb_matrix(mol2)
eig1 = get_eigenvalues_from_matrix(mat1, dim=max_n_atoms)
eig2 = get_eigenvalues_from_matrix(mat2, dim=max_n_atoms)
distance = np.sqrt(np.sum((eig1 - eig2) ** 2))
return distance
pyrrole = Chem.AddHs(Chem.MolFromSmiles('N1cccc1'))
thiophene = Chem.AddHs(Chem.MolFromSmiles('S1cccc1'))
AllChem.EmbedMolecule(pyrrole, AllChem.ETKDG())
AllChem.EmbedMolecule(thiophene, AllChem.ETKDG())
print(get_distance_mols_with_coulomb_matrix(ethanol, pyrrole))
print(get_distance_mols_with_coulomb_matrix(pyrrole, thiophene))
在本文中,各自的距離分別為30.7和306.9,但是由於使用了通過DFT優化的三維結構,因此這種偏差量是可以接受的。
庫侖矩陣在QM7數據集中顯示化學空間 (pybel.readfile(format, file))
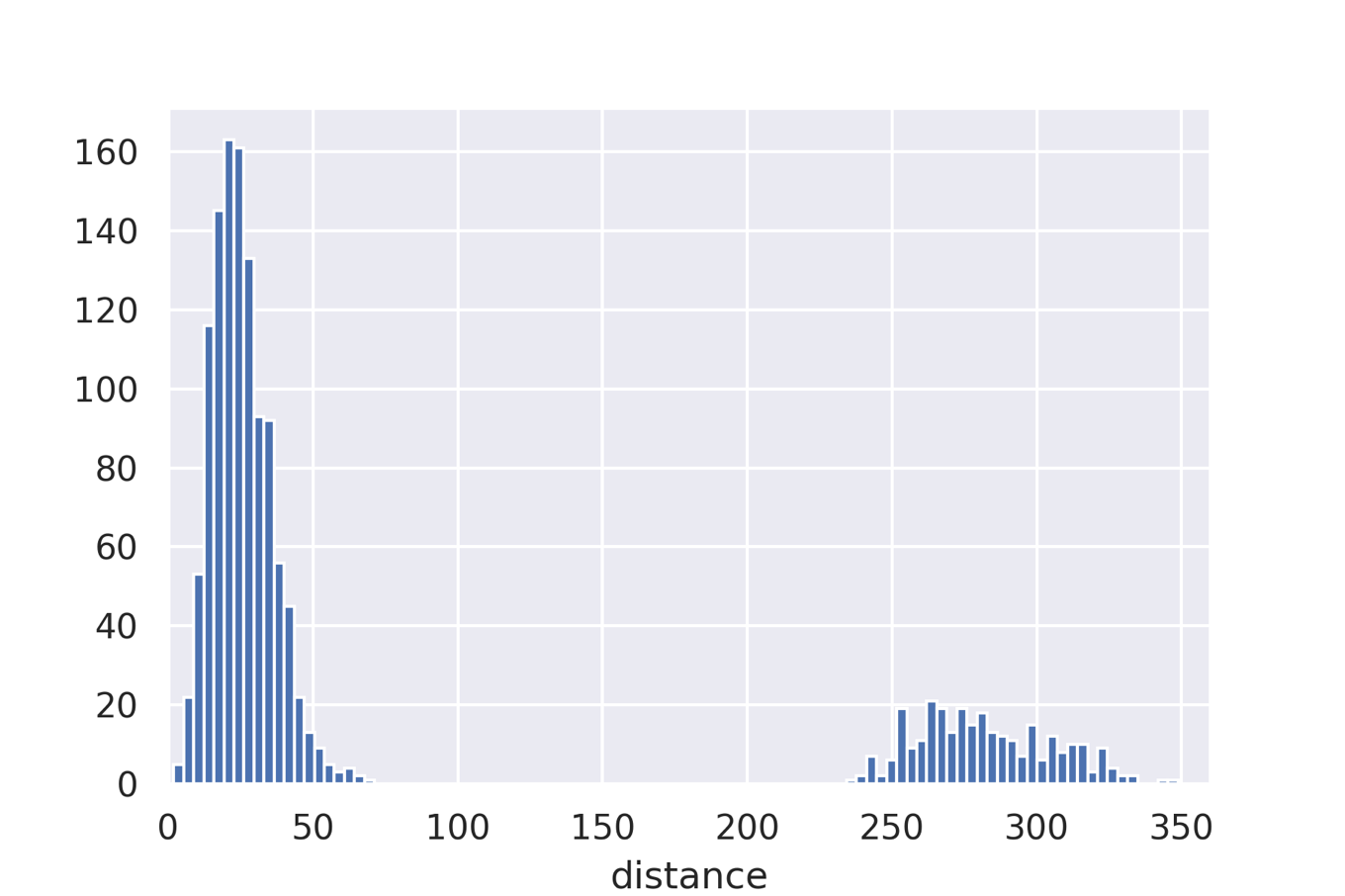
然後,使用文章“ QM9是用於基於量子化學計算的機器學習的大規模數據集”中介紹的QM7數據集,計算所有分子的距離,並獲得本文圖1所示的直方圖。 讓我們來創建它。 這次,我們使用QC存檔中託管的數據。
坐標數據是“分子”文件夾中按XYZ格式分為每個分子的文件。 在RDKit中,無法原樣讀取XYZ格式並使其成為MOL對象,因此在處理之前,請使用Open Babel將其轉換為mol格式。
XYZ格式在文章“ XYZ格式和Z矩陣是代表分子三維結構的輸入格式”中進行了描述,Open Babel在文章“使用Open Babel轉換化學信息的文件格式”中進行了描述。 請參考。
在下面的代碼中
1. 獲取XYZ文件列表
2. 將XYZ格式轉換為mol格式並轉換為RDKit MOL對象
3. 使用之前創建的函數獲取距離矩陣
4. 由於距離矩陣是對稱矩陣,因此提取了上三角部分,並且僅將非零部分聚合併可視化。
在過程中進行處理。
import pandas as pd
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns
sns.set()
import os
import pybel
cwd = os.getcwd()
folder = os.path.join(cwd, 'molecules')
files = os.listdir(folder)
mols = []
for file in files:
pybel_mol = [x for x in pybel.readfile('xyz', os.path.join(folder, file))]
rdkit_mol = Chem.MolFromMolBlock(pybel_mol[0].write('mol'), removeHs=False)
mols.append(rdkit_mol)
distant_mat = np.zeros((len(mols), len(mols)))
for i, mol1 in enumerate(mols):
for j, mol2 in enumerate(mols):
if i >= j:
distant_mat[i,j] = get_distance_mols_with_coulomb_matrix(mol1, mol2)
distant_mat[j,i] = distant_mat[i,j]
upper = np.triu(distant_mat)
upper_values = upper[np.nonzero(upper)].flatten()
plt.hist(upper_values, bins=100)
plt.xlabel('distance')
plt.xlim(0,360)
如論文中所示,獲得具有約30的峰和約280的峰的分佈。
 隨機庫侖矩陣 (numpy.linalg.norm(ndarray)) (numpy.argsort(ndarray))
隨機庫侖矩陣 (numpy.linalg.norm(ndarray)) (numpy.argsort(ndarray))
如上所述,由於改變分子中原子序數的操作,庫侖矩陣會更改其表示法,因此它不適合用作機器學習模型的輸入。
在發布QM7b數據集的論文中,作者報告了“隨機庫侖矩陣”作為該問題的解決方案。
QM7b的原始論文為以下論文。
“Machine learning of molecular electronic properties in chemical compound space” New J. Phys. 2013, 15, 095003.
在隨機庫侖矩陣中,不是所有原子的順序都是隨機的,而是根據以下方法改變原子的順序。
1. 對目標庫侖矩陣的每一行取二次範數
2. 從平均值為0且方差為1的標準正態分佈中獲取庫侖矩陣行數的樣本
3. 將2中獲得的噪聲矢量與通過排列1中獲得的範數而獲得的矢量相加,並以降序排列。
4. 按照索引的順序重新排列原始庫侖矩陣的順序,該索引給出以3降序排列的向量下面的代碼實現了這項工作。
RDKit CalcCoulombMatrix文檔說它可以計算多個隨機的庫侖矩陣,但是當前的實現似乎是一個普通的庫侖矩陣。
def gen_randomized_coulomb_matrix(matrix):
dim = len(matrix)
norm = np.linalg.norm(matrix, axis=1)
eps = np.random.randn(dim)
argsort = np.argsort(norm + eps)[::-1]
return matrix[argsort][:,argsort]
現在讓我們看一下按隨機庫侖矩陣排序的原子順序的含義。 嘗試使用三氟乙酸作為樣品。
cf3 = Chem.MolFromSmiles('FC(F)(F)C(=O)O')
cf3 = Chem.AddHs(cf3)
AllChem.EmbedMolecule(cf3, AllChem.ETKDGv3())
print(Chem.MolToXYZBlock(cf3))
每個原子的數目如下。
8
F -1.862577 0.741082 0.066203
C -0.906970 -0.229637 0.089326
F -0.970805 -0.988304 1.266901
F -1.038421 -1.077407 -1.017389
C 0.422649 0.410812 0.082517
O 0.479398 1.660903 0.058371
O 1.601289 -0.291838 0.101267
H 2.275438 -0.225610 -0.647196
mat_cf3 = coulomb_matrix(cf3)
print(mat_cf3)
|
庫侖矩陣如下。
[[97.53309975 39.63719848 35.42658225 35.65720106 23.38648228 28.61521425
19.9183092 2.08870123]
[39.63719848 36.8581052 38.50927649 38.56344315 24.39287334 20.47263766
19.13068059 1.8368131 ]
[35.42658225 38.50927649 97.53309975 35.41717176 23.45167162 22.13349794
24.75493838 2.3407392 ]
[35.65720106 38.56344315 35.41717176 97.53309975 22.90251923 21.74901541
24.22090596 2.61510138]
[23.38648228 24.39287334 23.45167162 22.90251923 36.8581052 38.35055838
34.97727325 2.87007732]
[28.61521425 20.47263766 22.13349794 21.74901541 38.35055838 73.51669472
28.41310326 2.9644856 ]
[19.9183092 19.13068059 24.75493838 24.22090596 34.97727325 28.41310326
73.51669472 7.92483514]
[ 2.08870123 1.8368131 2.3407392 2.61510138 2.87007732 2.9644856
7.92483514 0.5 ]]
print(gen_randomized_coulomb_matrix(mat_cf3))
隨機庫侖矩陣為
[[97.53309975 35.42658225 35.65720106 28.61521425 19.9183092 39.63719848
23.38648228 2.08870123]
[35.42658225 97.53309975 35.41717176 22.13349794 24.75493838 38.50927649
23.45167162 2.3407392 ]
[35.65720106 35.41717176 97.53309975 21.74901541 24.22090596 38.56344315
22.90251923 2.61510138]
[28.61521425 22.13349794 21.74901541 73.51669472 28.41310326 20.47263766
38.35055838 2.9644856 ]
[19.9183092 24.75493838 24.22090596 28.41310326 73.51669472 19.13068059
34.97727325 7.92483514]
[39.63719848 38.50927649 38.56344315 20.47263766 19.13068059 36.8581052
24.39287334 1.8368131 ]
[23.38648228 23.45167162 22.90251923 38.35055838 34.97727325 24.39287334
36.8581052 2.87007732]
[ 2.08870123 2.3407392 2.61510138 2.9644856 7.92483514 1.8368131
2.87007732 0.5 ]]
為了詳細研究隨機改組的原子,下面的代碼生成五次隨機化的庫侖矩陣,僅關注原子的順序。
def return_sorted_index(matrix):
dim = len(matrix)
norm = np.linalg.norm(matrix, axis=-1)
eps = np.random.randn(dim)
argsort = np.argsort(norm + eps)[::-1]
return argsort
atom_list = [atom.GetSymbol() for atom in cf3.GetAtoms()]
for _ in range(5):
atoms = return_sorted_index(mat_cf3)
print(pd.Series(atom_list)[atoms])
2 F
0 F
3 F
5 O
6 O
1 C
4 C
7 H
dtype: object
3 F
0 F
2 F
6 O
5 O
1 C
4 C
7 H
dtype: object
2 F
3 F
0 F
5 O
6 O
1 C
4 C
7 H
dtype: object
0 F
2 F
3 F
5 O
6 O
1 C
4 C
7 H
dtype: object
3 F
0 F
2 F
6 O
5 O
1 C
4 C
7 H
dtype: object
通過創建隨機庫侖矩陣重排的所有原子的順序為“氟,氧,碳,氫”。 如果查看三個氟之間的順序,您會發現三個氟被平等對待並隨機排列。 氧氣也是如此。 另一方面,碳的順序每次都相同。
因此,在隨機庫侖矩陣中,僅在具有對稱性的化學等效原子內改變順序。 該論文的作者報告說,當使用這種隨機化的庫侖矩陣作為輸入時,機器學習模型的準確性要比簡單地按原子序數重新排列庫侖矩陣時的機器學習模型更高。
結論
這次,關於``庫侖矩陣是表達不變於分子旋轉和平移的化合物的方法''的主題,
- 什麼是庫侖矩陣
- 使用RDKit的庫侖矩陣計算方法
- 使用numpy實現庫侖矩陣計算
- 使用庫侖矩陣定義和實現分子間距離
- 隨機庫侖矩陣的描述與實現
特別是對分子進行向量化處理時,重要的概念是考慮平移和旋轉操作的不變性,而不僅僅是庫侖矩陣。
作為源自庫侖矩陣和自然語言處理的思想的分子向量化方法,有一種考慮分子中一組鍵的``Bag of Bonds(BoB)''。下次我想看這個。請注意,RDKit當前不具有查找BoB的功能,但是根據GitHub PR,它將很快實現。
Bag of Bonds的原始文件如下。
“Machine Learning Predictions of Molecular Properties: Accurate Many-Body Potentials and Nonlocality in Chemical Space” J. Phys. Chem. Lett. 2015, 6, 2326-2331.
參考
https://future-chem.com/coulomb-matrix/











