神經網絡是受人類brian功能啟發的演算法。 一般來說,當你睜開眼睛時,你所看到的就是所謂的數據,由大腦中的Nuerons(數據處理細胞)處理,並識別你身邊的東西。 這就是神經網絡的工作方式。 它們獲取大量數據,處理數據(從數據中提取模式),並輸出它的內容。
What they do ?
神經網絡有時被稱為人工神經網絡(ANN),因為它們不像大腦中的神經元那樣自然。 它們巧妙地模仿了神經網絡的本質和功能。 ANN由大量高度互連的處理元件(神經元)組成,它們協同工作以解決特定問題。
神經網絡(NN)是通用函數近似(universal function approximaters),因此神經網絡可以學習任何函數f()的近似值。
y = f(x)
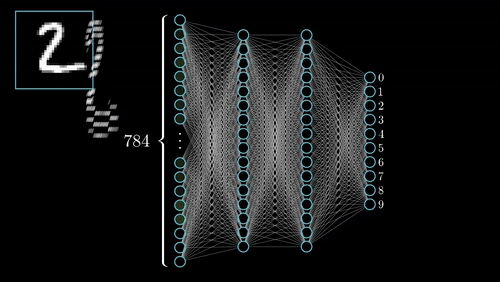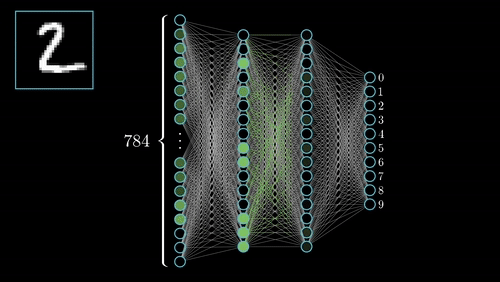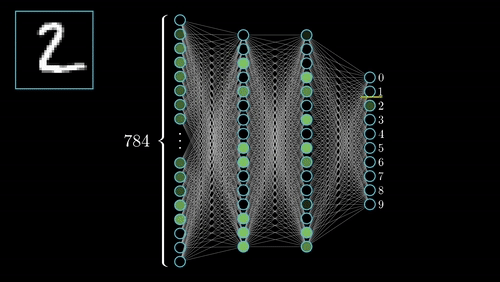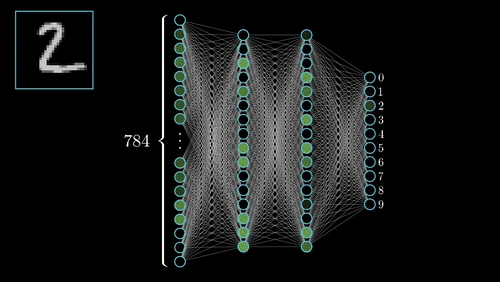
你可以在這裡查看其他幾個神經網絡。
[補充1] Universal approximation theorem

Universal approximation theorem:用一層隱藏層的神經網絡,若使用的激勵函數具有單調遞增、有上下界、非常數且連續的性質,則總是存在一個擁有有限N個神經元的單隱藏層神經網絡可以無限逼近這個連續函數(鮑萊耳可測函數)。
但這個定理沒有說在這個神經網路裡的參數要怎麼學,只知道隱藏層的寬度會隨著問題複雜度提升變得非常大,因此,增加網絡深度的原因正是為了可以用更少的參數量實現同樣的逼近。
[補充2] 無免費午餐定理 No Free Lunch Theorem

無免費午餐定理:最佳化演算法的總體效能並無法定義孰優孰劣,也就是說,不存在一個對所有問題具有普遍優勢的演算法;換一個樂觀一點的說法:一定存在某個演算法在解某種問題時表現最好。
這可以回答激勵函數選擇上,或任意最佳化演算法設計上的問題;不可能有一個最好的最佳化演算法設計適合所有的任務。
參考
https://mropengate.blogspot.com/2017/02/deep-learning-role-of-activation.html
Why use Neural networks?
神經網絡具有從複雜或不精確的數據中獲得意義的顯著能力,可用於提取模式並檢測過於複雜而無法被人類或其他計算機技術注意到的趨勢。 訓練有素的神經網絡被認為是分析類別中的“專家”。 然後,在感興趣的新情況的情況下可以使用該專家提供預測並回答“假設”問題。
其他優點包括:
1.Adaptive learning:根據訓練或初始經驗提供的數據,學習如何完成任務的能力。
2.Self-Organisation:人工神經網絡可以創建自己的組織(organisation)或在學習期間收到資訊的表示(representation)。
Network layers
人工神經網絡最常見類型由三個單元groups或單元layers組成:一層“輸入”單元連接到一層“隱藏”單元,它連接到一層“輸出”單元。(見圖4.1)
Input units:輸入單位的行為表示饋入網絡的原始資訊(raw information)。 這也稱為輸入層。
Hidden units:每個隱藏單位的行為由輸入單位的行為和輸入與隱藏單位之間的權重決定。 這也稱為隱藏層。
Output units:輸出單位的行為取決於隱藏單位的行為以及隱藏單位和輸出單位之間的權重。 這也稱為輸出層。
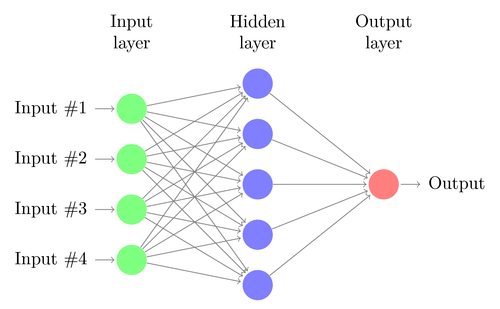
這種簡單類型的網絡很有趣,因為隱藏單元可以自由構建input的representations。 輸入和隱藏單元之間的權重確定每個隱藏單元何時處於active,因此透過修改這些權重,隱藏單元可以選擇它表現出什麼特徵。
在我們研究整個/深度神經網絡之前,讓我們看一下單個神經元。
A Single Neuron
神經網絡中的基本計算單元是神經元,通常稱為節點(node)或單元(unit)。 它從一些其他節點或external source接收input來計算output。 每個input都有一個相關的權重(w),它是根據其對其他input的相對重要性來分配的。 節點將應用函數f來加權input總和,如下圖所示。
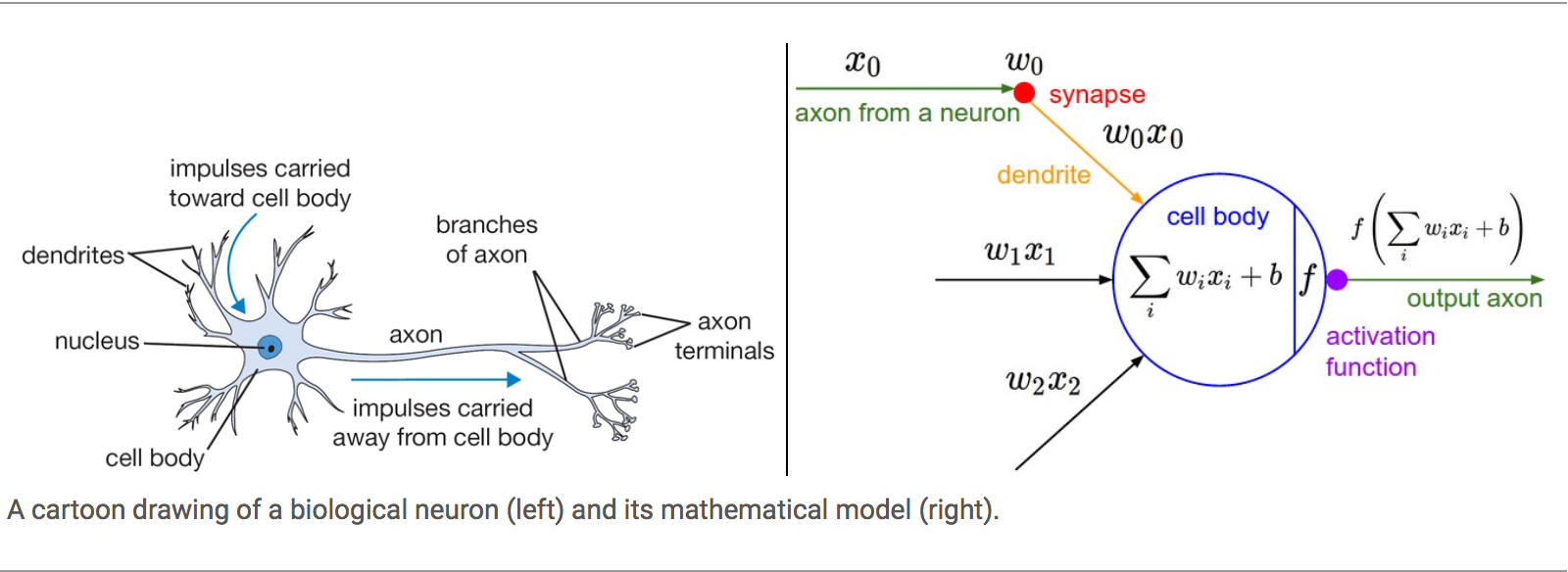
上述網絡採用數字input X1和X2,並具有與這些input相關的權重w1和w2。 另外,存在另一個與input 1相關聯的權重b(稱為Bias)。
Activation function:
來自神經元的output Y的計算如上圖所示。 函數f是非線性的,稱為激活函數(Activation Function)。 激活功能的目的是將非線性(non-linearity)引入神經元的output。 這很重要,因為大多數現實世界的數據都是非線性的,我們希望神經元學習這些非線性表示。
每個激活函數(或非線性)採用單個數字並對其執行某個公式的數學運算。 在實際中您可能會遇到幾種激活功能:
Sigmoid:得到real-valued input並將其壓縮到0到1之間
σ(x) = 1 / (1 + exp(−x))
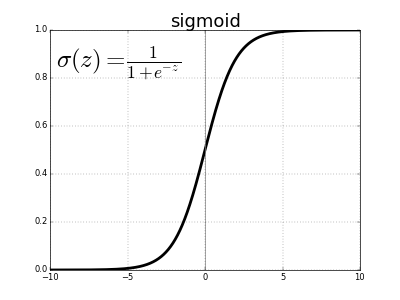
Softmax function:在分類工作中,我們通常使用Softmax函數作為多層感知器輸出層中的激活函數,以確保輸出是概率,它們加起來為1. Softmax函數採用任意real-valued分數的向量,並將其壓縮為0到1之間的向量值,總和為1。 那麼,在這種情況下,
Probability (Pass) + Probability (Fail) = 1
tanh:得到real-valued input並將其壓縮到範圍[-1,1]
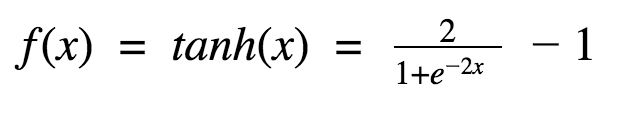
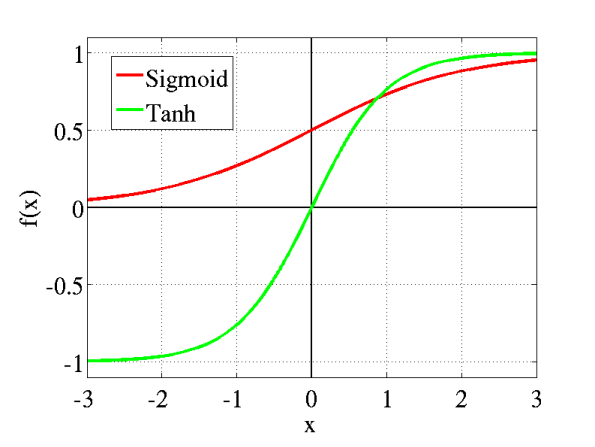
ReLU:ReLU代表整流線性單元(Rectified Linear Unit)。 它需要一個real-valued input,並將其閾值設為零(將負值替換為零)
f(x) = max(0, x)
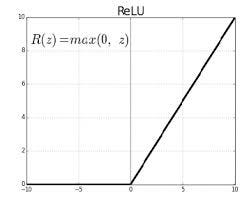
下圖顯示了其他幾種激活函數。
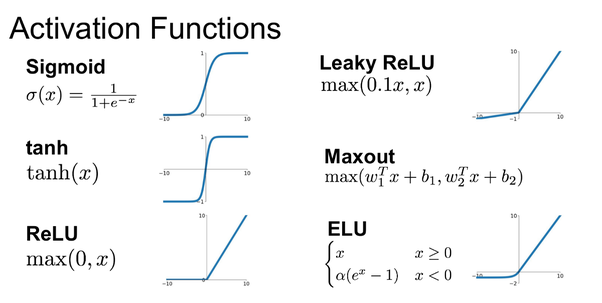
Bias的重要性:偏差的主要功能是為每個節點提供可訓練的常數值(除了節點接收的正常輸入之外)。 請參閱此連結以了解有關bias在神經元中的作用的更多資訊。
每個神經網絡有兩個主要部分:
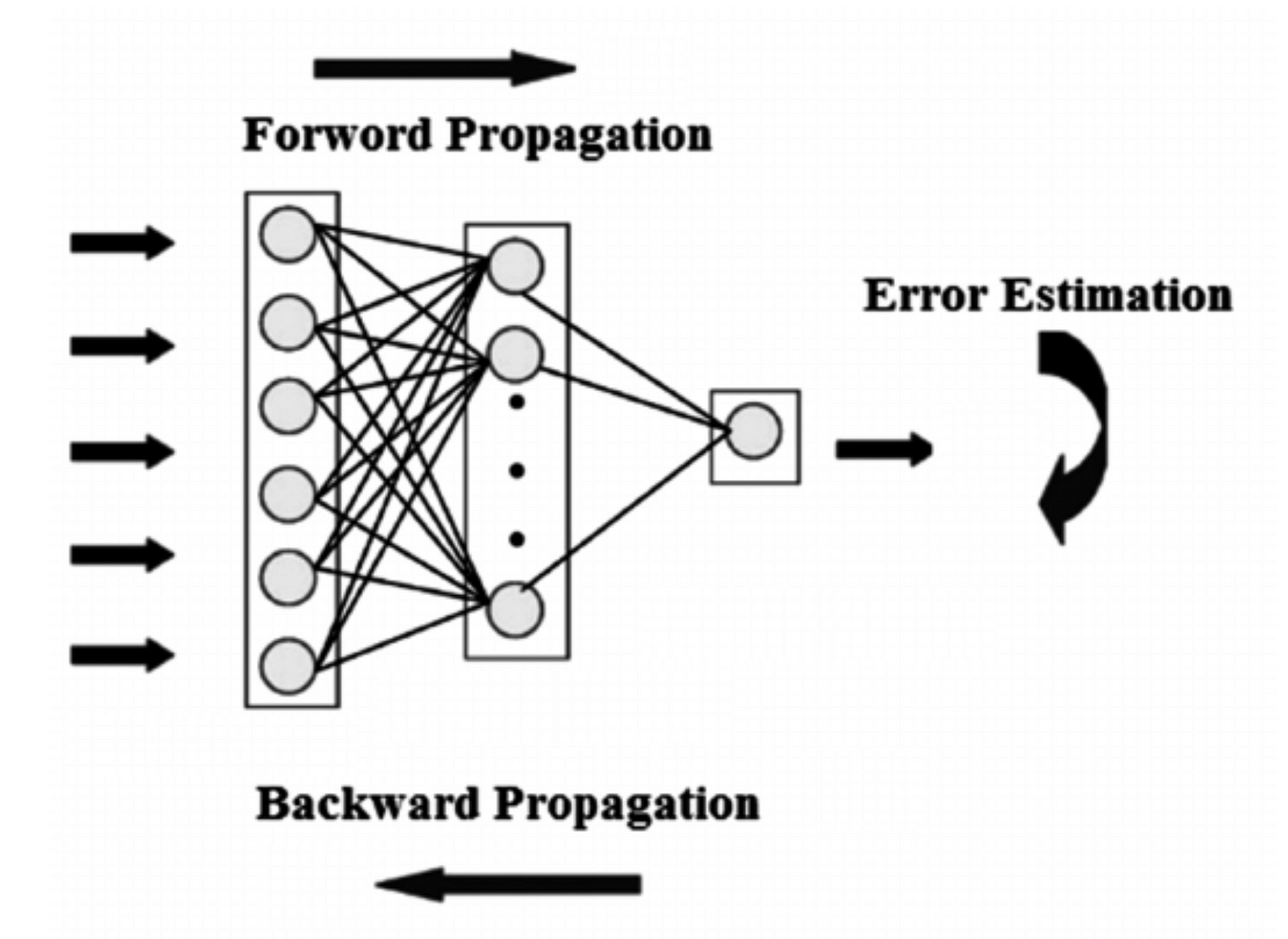
1.前饋傳播/前向傳播(Feed Forward Propogation/Forward Propogation)。
2.向後傳播/反向傳播(Backward Propogation/Back propogation)。
讓我們看看每個部分。
Feed Forward Propogation:
網絡中的所有權重都是隨機分配的。假設從輸入到該節點的連接的權重是w1,w2和w3。
然後網絡將第一個訓練範例作為輸入(我們知道對於輸入35和67,Pass的概率是1)。
輸入網絡= [35,67]
網絡想要的輸出(目標)= [1,0]
然後,可以如下計算輸出V(f是諸如sigmoid的激活函數):
V = f(1 * w1 + 35 * w2 + 67 * w3)
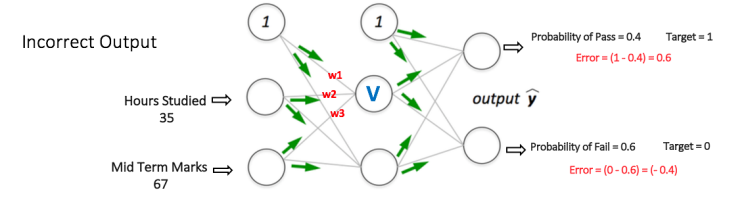
類似地,還計算來自隱藏層中的另一節點的輸出。隱藏層中兩個節點的輸出充當輸出層中兩個節點的輸入。這使我們能夠從輸出層中的兩個節點計算輸出概率。
假設輸出層中兩個節點的輸出概率分別為0.4和0.6(因為權重是隨機分配的,輸出也是隨機的)。我們可以看到計算的概率(0.4和0.6)與期望的概率(分別為1和0)相差很遠,因此圖5中的網絡被稱為具有“不正確的輸出”。
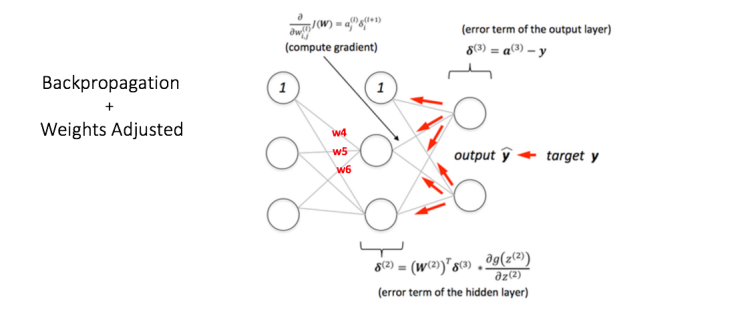
Back Propagation and Weight Updation:
我們計算輸出節點處的總誤差,並使用Backpropagation通過網絡將這些誤差傳播回來計算梯度。 然後我們使用諸如Gradient Descent之類的優化方法來“調整”網絡中的所有權重,目的是減少輸出層的誤差。
假設與所考慮的節點相關聯的新權重是w4,w5和w6(在反向傳播和調整權重之後)。
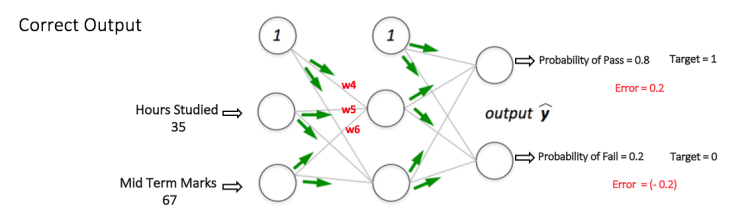
如果我們現在再次向網絡input相同的範例,則網絡應該比以前更好地執行,因為現在已經調整了權重以最小化預測中的錯誤。 如圖7所示,與之前的[0.6,-0.4]相比,輸出節點處的誤差現在減少到[0.2,-0.2]。 這意味著我們的網絡已經學會正確分類我們的第一個訓練範例。
我們在數據集中使用所有其他訓練範例重複此過程。 然後,我們的網絡可以說是已經學會了這些例子。
如果我們現在想要預測一個學習25個小時並且在學期中有70個分數的學生是否會通過最後一個學期,我們將通過前向傳播步驟找到及格和不及格的輸出概率。
以上避免了數學方程式和諸如“Gradient Descent”之類的概念的解釋。有關Backpropagation算法的更多數學討論,請參閱此連接。
參考
https://medium.com/@purnasaigudikandula/a-beginner-intro-to-neural-networks-543267bda3c8